Tổng hợp các lệnh lập trình tính toán trên MATLAB
Trong quá trình giải bài tập mùa dịch Covid-19 mình có tổng hợp lại một số lệnh lập trình đại số giúp các thao tác biến đổi, xử lí phương trình và ma trận nhẹ nhàng hơn. Bài này sẽ liên tục được cập nhật khi mình tìm thêm các lệnh mới. Đầu tiên mình bắt đầu với các biến:
1. Một số biến mặc định: (biến không cần gán giá trị)
ans: lưu kết quả tính toán cuối cùng
pi: số Π = 3.14...
i hoặc j: biến số phức
eps: số epsilon
inf: vô cực (infinity)
NaN: vô định (not a number)
nargin/nargout: số đối số input/output của hàm
realmin: số thực dương nhỏ nhất
realmax: số thực dương lớn nhất
e: nhân luỹ thừa của 10 (5e2 = 5*102)
2. Một số lệnh:
clc: xoá màn hình
clear x: xoá biến x
clear x y z: xoá các biến x, y, z
clear: xoá tất cả các biến đã khai báo
gcd(a,b): tìm ước số chung lớn nhất
lcm(a,b): tìm bội số chung lớn nhất
mod(a,b): tìm số dư
primes(a): tìm các số nguyên tố đứng trước a
isprime(a): xác định a có phải là số nguyên tố hay không
4. Khai triển biểu thức đại số:
>> expand(expr)
Với expr là tích của các nhân tử cần khai triển, expr có thể là một biểu thức f(x) nào đó được khai báo từ trước. ví dụ:
5. Phân tích thành nhân tử: (ngược lại của lệnh 4)
>> factor(expr)
6. Rút gọn biểu thức:
>> simplify(expr)
>> simple(expr)
7. Giải phương trình:
>> solve(eqns)
Với eqns là phương trình f(x)=0 nào đó, f(x) được khai báo từ trước. Kết quả cho ra biểu thức nghiệm nếu các hệ số chưa được gán giá trị, ví dụ:
>> syms a b c x
>> f=a*x^2+b*x+c
>> solve(f)
Mặc định lệnh solve sẽ tìm x, nếu muốn tìm hệ số khác như hệ số b, ta dùng lệnh:
>> solve(f,b)
Đối với các phương trình f(x)≠0, ta chuyển vế để đưa về dạng f(x)=0 hoặc dùng các lệnh:
>> syms x real
>> solve('x^2+2*x=1')
hoặc
>> syms x real
>> solve(x^2+2*x==1)
8. Giải hệ phương trình:
>> solve(eqn1,eqn2,eqn3)
Với eqn1, eqn2, eqn3 là các phương trình được nhập vào từ trước, ví dụ:
Lưu ý: các phương trình eqn1, eqn2, eqn3 buộc phải nhập theo cú pháp này và kết thúc mỗi phương trình bằng dấu chấm phẩy.
Kết quả được lưu vào biến s (s lúc này đóng vai trò như một mảng), để xem kết quả ta lần lượt gọi các biến:
>> s.a
>> s.b
>> s.c
Nếu không gán kết quả cho biến s thì mặc định các kết quả lưu vào biến ans, khi đó ta xem kết quả bằng cách gọi các biến:
>> ans.a
>> ans.b
>> ans.c
9. Tìm giới hạn hàm số:
>> limit(f,x,point)
Với point là điểm mà tại đó cần tính giới hạn hàm số, ví dụ:
Giới hạn tại x=0, ta dùng lệnh:
>> limit(f,x,0) hoặc >> limit(f)
Giới hạn tại x=a, ta dùng lệnh:
>> limit(f,x,a) hoặc >> limit(f,a)
Giới hạn tại vô cùng:
>> limit(f,x,inf)
10. Tính đạo hàm một biến:
>> diff(f(x))
11. Khai triển Taylor:
>> taylor(f,'Order',m)
Ví dụ: Khai triển y=sin(2x).cos(x) tới bậc 15 tại x=0
>> approx=taylor(sin(2*x)*cos(x),'Order',15)
2. Các ma trận có sẵn:
Với m,n là kích thước của ma trận.
3. Nhập ma trận từ file .dat:
>> load file_name.dat
Ví dụ: có file matrix.dat có nội dung sau:
Sau khi dùng lệnh load, ma trận trong file matrix.dat sẽ được lưu vào biến matrix.
4. Nhập ma trận từ file .m:
>> file_name
Ví dụ: có file matrix.m từ trình soạn thảo của matlab có nội dung sau:
>> matrix
5. Trích xuất phần tử trong ma trận:
>> A(i,j)
Với A là tên ma trận, (i,j) là vị trí dòng, cột của phần tử.
hoặc
>> A(n)
Với n là số thứ tự của phần tử duyệt theo cột từ trên xuống dưới, từ trái qua phải.
6. Thêm thành phần vượt khỏi kích thước ma trận:
>> A(i,j)=n
Với (i,j) là vị trí chứa thành phần cần thêm, n là giá trị của thành phần. Các vị trí mới còn lại mặc định bằng 0
7. Lấy giá trị và phần tử:
Ví dụ: nhập ma trận A từ file matrix.dat ở phía trên.
>> 1:10
ans =
1 2 3 4 5 6 7 8 9 10
>> 100:-7:50 //các số nguyên chạy lùi bước 7 từ 100 đến 50
ans =
100 93 86 79 72 65 58 51
>> A(1,1:3) //tổng các phần tử vị trí 1 đến 3 trong cột 1
ans =
12
>> A(1,:) //toàn bộ phần tử của dòng 1
ans =
1 2 3
>> A(end,1) //phần tử cuối cùng của cột 1
ans =
7
>> A(2,[3,1]) //phần tử thứ 3 và thứ 1 của dòng 2
ans =
6 4
>> x=[2 1 5 8] //tạo ma trận x có 1 hàng
>> x=([2,4]) //phần tử thứ 2 và thứ 4 của ma trận x
ans =
1 8
8. Ghép 2 ma trận:
B có cùng số hàng với A, ví dụ:
Với C có cùng số cột với A, ví dụ:
A =
1 2 3
A=
1 3
10. Tổng các cột của ma trận:
>> sum(A)
Ví dụ:
>> A'
(Còn nữa)
ans: lưu kết quả tính toán cuối cùng
pi: số Π = 3.14...
i hoặc j: biến số phức
eps: số epsilon
inf: vô cực (infinity)
NaN: vô định (not a number)
nargin/nargout: số đối số input/output của hàm
realmin: số thực dương nhỏ nhất
realmax: số thực dương lớn nhất
e: nhân luỹ thừa của 10 (5e2 = 5*102)
2. Một số lệnh:
clc: xoá màn hình
clear x: xoá biến x
clear x y z: xoá các biến x, y, z
clear: xoá tất cả các biến đã khai báo
gcd(a,b): tìm ước số chung lớn nhất
lcm(a,b): tìm bội số chung lớn nhất
mod(a,b): tìm số dư
primes(a): tìm các số nguyên tố đứng trước a
isprime(a): xác định a có phải là số nguyên tố hay không
I. PHƯƠNG TRÌNH:
3. Tính toán biểu thức dạng chuỗi:- Tính tổng:
- Tính tích:
4. Khai triển biểu thức đại số:
>> expand(expr)
Với expr là tích của các nhân tử cần khai triển, expr có thể là một biểu thức f(x) nào đó được khai báo từ trước. ví dụ:
>> factor(expr)
6. Rút gọn biểu thức:
>> simplify(expr)
>> simple(expr)
7. Giải phương trình:
>> solve(eqns)
Với eqns là phương trình f(x)=0 nào đó, f(x) được khai báo từ trước. Kết quả cho ra biểu thức nghiệm nếu các hệ số chưa được gán giá trị, ví dụ:
>> syms a b c x
>> f=a*x^2+b*x+c
>> solve(f)
>> solve(f,b)
Đối với các phương trình f(x)≠0, ta chuyển vế để đưa về dạng f(x)=0 hoặc dùng các lệnh:
>> syms x real
>> solve('x^2+2*x=1')
hoặc
>> syms x real
>> solve(x^2+2*x==1)
8. Giải hệ phương trình:
>> solve(eqn1,eqn2,eqn3)
Với eqn1, eqn2, eqn3 là các phương trình được nhập vào từ trước, ví dụ:
Kết quả được lưu vào biến s (s lúc này đóng vai trò như một mảng), để xem kết quả ta lần lượt gọi các biến:
>> s.a
>> s.b
>> s.c
Nếu không gán kết quả cho biến s thì mặc định các kết quả lưu vào biến ans, khi đó ta xem kết quả bằng cách gọi các biến:
>> ans.a
>> ans.b
>> ans.c
9. Tìm giới hạn hàm số:
>> limit(f,x,point)
Với point là điểm mà tại đó cần tính giới hạn hàm số, ví dụ:
Giới hạn tại x=0, ta dùng lệnh:
>> limit(f,x,0) hoặc >> limit(f)
Giới hạn tại x=a, ta dùng lệnh:
>> limit(f,x,a) hoặc >> limit(f,a)
Giới hạn tại vô cùng:
>> limit(f,x,inf)
10. Tính đạo hàm một biến:
>> diff(f(x))
11. Khai triển Taylor:
>> taylor(f,'Order',m)
Ví dụ: Khai triển y=sin(2x).cos(x) tới bậc 15 tại x=0
>> approx=taylor(sin(2*x)*cos(x),'Order',15)
II. MA TRẬN
1. Nhập ma trận:- Ma trận nằm trong cặp dấu []
- Dấu ; kết thúc một hàng
- Các phần từ trên cùng một hàng cách nhau bằng khoảng trắng
- Ma trận 0:
Với m,n là kích thước của ma trận.
- Ma trận 1:
- Ma trận đơn vị:
- Ma trận đường chéo:
- Ma phương:
- Ma trận số thực ngẫu nhiên từ 0 đến 1, nhân với hệ số để được ma trận số nguyên:
3. Nhập ma trận từ file .dat:
>> load file_name.dat
Ví dụ: có file matrix.dat có nội dung sau:
1 2 3
4 5 6
7 8 9
>> load matrix.dat
4. Nhập ma trận từ file .m:
>> file_name
Ví dụ: có file matrix.m từ trình soạn thảo của matlab có nội dung sau:
A=[1 2 3
4 5 6
7 8 9]
>> matrix
5. Trích xuất phần tử trong ma trận:
>> A(i,j)
Với A là tên ma trận, (i,j) là vị trí dòng, cột của phần tử.
hoặc
>> A(n)
Với n là số thứ tự của phần tử duyệt theo cột từ trên xuống dưới, từ trái qua phải.
6. Thêm thành phần vượt khỏi kích thước ma trận:
>> A(i,j)=n
Với (i,j) là vị trí chứa thành phần cần thêm, n là giá trị của thành phần. Các vị trí mới còn lại mặc định bằng 0
7. Lấy giá trị và phần tử:
Ví dụ: nhập ma trận A từ file matrix.dat ở phía trên.
>> 1:10
ans =
1 2 3 4 5 6 7 8 9 10
>> 100:-7:50 //các số nguyên chạy lùi bước 7 từ 100 đến 50
ans =
100 93 86 79 72 65 58 51
>> A(1,1:3) //tổng các phần tử vị trí 1 đến 3 trong cột 1
ans =
12
>> A(1,:) //toàn bộ phần tử của dòng 1
ans =
1 2 3
>> A(end,1) //phần tử cuối cùng của cột 1
ans =
7
>> A(2,[3,1]) //phần tử thứ 3 và thứ 1 của dòng 2
ans =
6 4
>> x=[2 1 5 8] //tạo ma trận x có 1 hàng
>> x=([2,4]) //phần tử thứ 2 và thứ 4 của ma trận x
ans =
1 8
8. Ghép 2 ma trận:
- Thêm cột:
B có cùng số hàng với A, ví dụ:
- Thêm hàng:
Với C có cùng số cột với A, ví dụ:
9. Xoá:
- Xoá dòng:
A =
1 2 3
- Xoá cột:
A=
1 3
10. Tổng các cột của ma trận:
>> sum(A)
Ví dụ:
11. Ma trận chuyển vị:
>> A'
(Còn nữa)
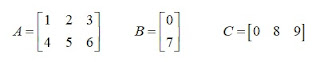
Đăng nhận xét